掷n个骰子点数的概率分布
求n个骰子和为s的概率
Gossip
前几周偶然和同学聊起依图的面试,说起面试官提出了一个问题:投掷N个均匀的骰子,请求出最后点数之和为S的概率。联系到概率论的知识,先把问题抽象一下,随机变量$X$的概率分布如下:
| $X$ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P($X$) | $\frac16$ | $\frac16$ | $\frac16$ | $\frac16$ | $\frac16$ | $\frac16$ |
$n$个随机变量$X_1,X_2,\cdots.X_n$均服从$X$的概率分布且相互独立,求随机变量$S=X_1+X_2+\cdots+X_n$的概率分布。显然$S$的取值介于$n$到$6n$之间,但是$S$是一个离散的随机变量,这是一个可加序列。我们先来看看2个骰子的情况,如果把$X_1$和$X_2$分别作为二维坐标系的轴,我们可以画出下面的图
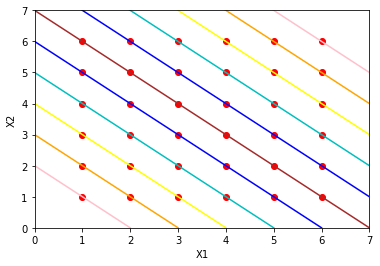
11条斜线代表着$X_1+X_2$的等值线,直线的截距即为2个骰子时的$S$,统计下每条直线上的点,得到的分布如下:
| $S$ | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| $\mathrm{P}(S)$ | $\frac1{36}$ | $\frac2{36}$ | $\frac3{36}$ | $\frac4{36}$ | $\frac{5}{36}$ |
| 7 | 8 | 9 | 10 | 11 | 12 |
| $\frac6{36}$ | $\frac5{36}$ | $\frac4{36}$ | $\frac3{36}$ | $\frac2{36}$ | $\frac1{36}$ |
同样,再试试3个骰子的情况,在三维的空间下用$X_1,X_2,X_3$来作为三个坐标轴,画出图形
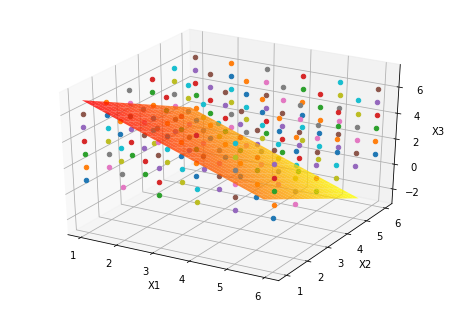
图中橙色的平面为$X_1+X_2+X_3=9$,散点即为各种投掷结果。从图中也可以看出,在3个骰子情况下,用图解统计的方法去解决已经有些吃力了。
于是不得不从另一个角度去看,考虑$\mathrm{P}(S=n)$,很显然,这种情况下每次投掷都是1,所以概率为$\frac1{6^n}$,相对地,$\mathrm{P}(S=6n)$也是一样。由此我们大概能知道$S$的分布是对称的。如果再试着写一下$S=n$后面的一个概率,大概能得到下面的式子:
\[\mathrm{P}(S=n+1)=\frac{C^1_n}{6^n}=\mathrm{P}(S=6n-1)\]因为$S=n+1$时就是$n-1$个一点和$1$个二点,这种情况一共有$C_n^1$种。对于$S=n+2$的情况,就更复杂一点,$n-2$个一点和$2$个二点,或者$n-1$个一点和$1$个三点。问题到这里我们大概能看到,这个问题其实是一个寻找排列组合的问题。
Solution
对于$n\le k\le 6n$,$\mathrm{P}(S_n=k)$(其中$S_n=k$表示$n$个骰子点数之和为$k$)可以进行分解如下:
\[\mathrm{P}(S_n=k)=\frac16\sum_{i=1}^6\mathrm{P}(S_{n-1}=k-i)\]若$k-i<n-1$或$k-i>6n-6$,则$\mathrm{P}(S_{n-1}=k-i)=0$。运用动态规划的方法,递归地计算,分配一个数组来存储中间变量,可以大大减少计算的时间。至于更高级的数学解法,还是等着抛砖引玉了。
| 微信(WeChat Pay) | 支付宝(AliPay) |

|

|
| 比特币(Bitcoin) | 以太坊(Ethereum) |

|

|
| 以太坊(Base) | 索拉纳(Solana) |

|

|